We have already studied the quadratic formula,
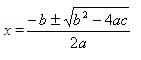
The term which is inside the square root symbol is called the discriminant.
It is used to determine the nature of the roots of a quadratic equation. We can also determine the number of real roots for a quadratic equation with this number. The following table will give us the relation between the discriminant and the nature of the roots.
Discriminant | Nature of roots | Number of real roots |
b2 - 4ac > 0 | Two real roots | 2 |
b2 - 4ac = 0 | Double root | 1 |
b2 - 4ac < 0 | No real roots | 0 |
Example 1:
Find the discriminant value for the equation x2 + 5x + 6 = 0 and determine the number of real roots.
Solution:
Step 1:
Given equation is x2 + 5x + 6 = 0.
It is in the form ax2 + bx + c = 0, where a = 1, b = 5, and c = 6.
Step 2:
The discriminant = b2 - 4ac
b2 - 4ac = (5)2 - 4(1)(6) = 25 - 24 = 1 > 0
=> The equation has two real roots.
=> The graph of this equation will touch the x-axis twice.
Step 3:
So, the given equation has two real roots.
Example: 2
Find the discriminant value of x2 - 12x + 36 = 0 and determine the number of real roots.
Solution:
Step 1:
Given equation is x2 - 12x + 36 = 0.
It is in the form ax2 + bx + c = 0 where, a = 1, b = -12, and c = 36.
Step 2:
Discriminant = b2 - 4ac = (-12)2 - 4(1)(36) = 144 - 144 = 0
=> The equation has a double root.
=> The graph of this equation touches the x-axis in only one point.
Step 3:
So, the given equation has a double root.
Example: 3
Find the discriminant value 2x2 + x + 3 = 0 and determine the number of real roots.
Solution:
Step 1:
The given quadratic equation is 2x2 + x + 3 = 0.
It is in the form ax2 + bx + c = 0 where, a = 2, b = 1, and c = 3.
Step 2:
b2 - 4ac = (1)2 - 4(2)(3) = 1 - 24 = -23 < 0
=> The equation has no real roots.
=> The graph of this equation does not touch the x-axis.
Step 3:
So, the given quadratic equation has no real roots.
Related Articles: