This tutorial explains how to find the least common multiple (some people say lowest common multiple) of any two or three given numbers with detailed example. LCM worksheets provided at the end of tutorial to practice.
LCM for any two numbers:
Least common multiple (LCM) for any given numbers is a lowest number which is divisible by all the numbers taken into account. Not clear??? Look at the following example.
Take any two numbers say 3 and 5. Now list the numbers that are divisible by both 3 and 5. We have 15, 30, 45, 60 and so on. Among those numbers which is smallest? Yes, you are right, it is 15. So, we can say that 15 is the lowest common multiple of 3 and 5. It is easy to find LCM for smaller numbers. Let us see how to find LCM for bigger numbers. Here is an example.
Find the LCM of 24 and 36:
It is really hard for anyone to find the number which is divisible by both 24 and 36. We are going to use the following trick to make it easy.
Use prime factor tree method to split numbers into product of primes.
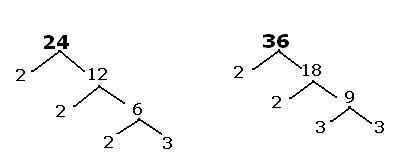
Taking only the primes, we can write 24 and 36 as below.
24 = 2 * 2 * 2 * 3
36 = 2 * 2 * 3 * 3
Take common primes once and then take uncommon primes as below:
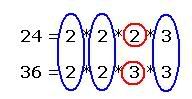
LCM = 2 * 2 * 3 * 2 * 3 = 72
72 is the least number which is divisible by both 24 and 36. Therefore 72 is the Least Common Multiple of 24 and 36.
LCM worksheets: Level 1
Find the least common multiple for the following pair of numbers.
a) 5, 7
b) 8, 9
c) 12, 15
d) 36, 48
e) 72, 96
LCM for any three numbers:
Procedure for finding least common multiple of any three numbers is not any more different that explained for two numbers. Anyway, here is an example for clear understanding.
Find the LCM of 12, 18 and 24:
Prime factorize 12, 18 and 24 using prime factor tree method.

What is our next step? Not sure? Refer previous example. Yes, you are right. We have to take common primes for all three numbers, then take common primes for any two numbers and then finally take all primes which is not yet considered.
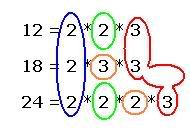
Circled with blue and red repeats in all three numbers. So, take it just once. We have 2 * 3.
Circled with green repeats in two places. Taking that once along with previous common factors, we have 2 * 3 * 2.
Look at the orange circle which never repeats in any places after picking all common primes.
Choosing them, we have 2 * 3 * 2 * 3 * 2.
Finally, we can say, LCM of 12, 18 and 24 = 2 * 3 * 2 * 3 * 2 = 72.
LCM worksheets: Level 2
What is the least common multiple for the given numbers?
a) 5, 7, 8
b) 8, 16, 32
c) 4, 12, 16
d) 24, 36, 42
e) 48, 56, 72
Few easy ways to find LCM:
1) If any two distinct numbers are prime, then LCM is product of those numbers.
For example, let’s take two prime numbers 5 and 7. LCM of 5 and 7 = 5 * 7 = 35
It works with any number of unique prime numbers.
Can you try the LCM of 5, 7 and 11?
LCM worksheets: Type 1
Find the lowest common multiple of the following.
a) 2, 3
b) 2, 3, 5
c) 7, 11
d) 11, 13
e) 3, 7
2) Are you familiar with Co-primes? Here is an example. Is 4 a prime? No. Is 9 a prime? No.
But 4 and 9 are co-prime. Have any guess why they are co-prime? I think you got the point. There are no common factors for 4 and 9. So, 4 and 9 are co-prime. LCM of co-prime numbers is just a product of those numbers. Do you understand this? What is the least common multiple for 4 and 9? Yes, you are right. It is just a product of 4 and 9. LCM of 4 and 9 = 4 * 9 = 36.
What is the LCM of 4, 9 and 25? Try it yourself.
What is the LCM of 3 and 4? Here 3 is prime, 4 is composite but both 3 and 4 are co-prime as it doesn’t contain common factors. So, LCM of 3 and 4 = 3 * 4 = 12
LCM worksheets: Type 2
Find the least common multiple for the given numbers:
a) 2, 9
b) 5, 6
c) 7, 8
d) 8, 11
e) 6, 11, 13
3) Now let’s take a number 4 and 8. What you can say about these numbers? 4 divides 8, isn’t it?
Therefore, LCM of 4 and 8 is just 8 itself. What is the LCM of 8 and 16? Yes, you are right. It is 16.
LCM worksheets: Type 3
Find the least common multiple of the following:
a) 5, 25
b) 2, 4, 8
c) 3, 9, 18
d) 6, 12
e) 14, 42
You may also interested in this: